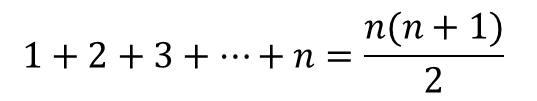AREAS OF KNOWLEDGE:
MATHEMATICS
MATHEMATICAL INDUCTION
Raphael (1509–1511) Euclid Detail from The School of Athens. Fresco. Apostolic Palace, Vatican City
“Mathematics, rightly viewed, possesses not only truth, but supreme beauty— a beauty cold and austere, like that of sculpture, without appeal to any part of our weaker nature, without the gorgeous trappings of painting or music, yet sublimely pure, and capable of a stern perfection such as only the greatest art can show. The true spirit of delight, the exaltation, the sense of being more than Man, which is the touchstone of the highest excellence, is to be found in mathematics as surely as poetry. ”
CLASS ACTIVITY I: REVISIT PASCAL'S TRIANGLE
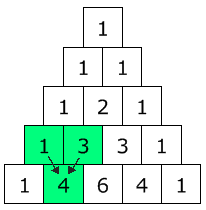
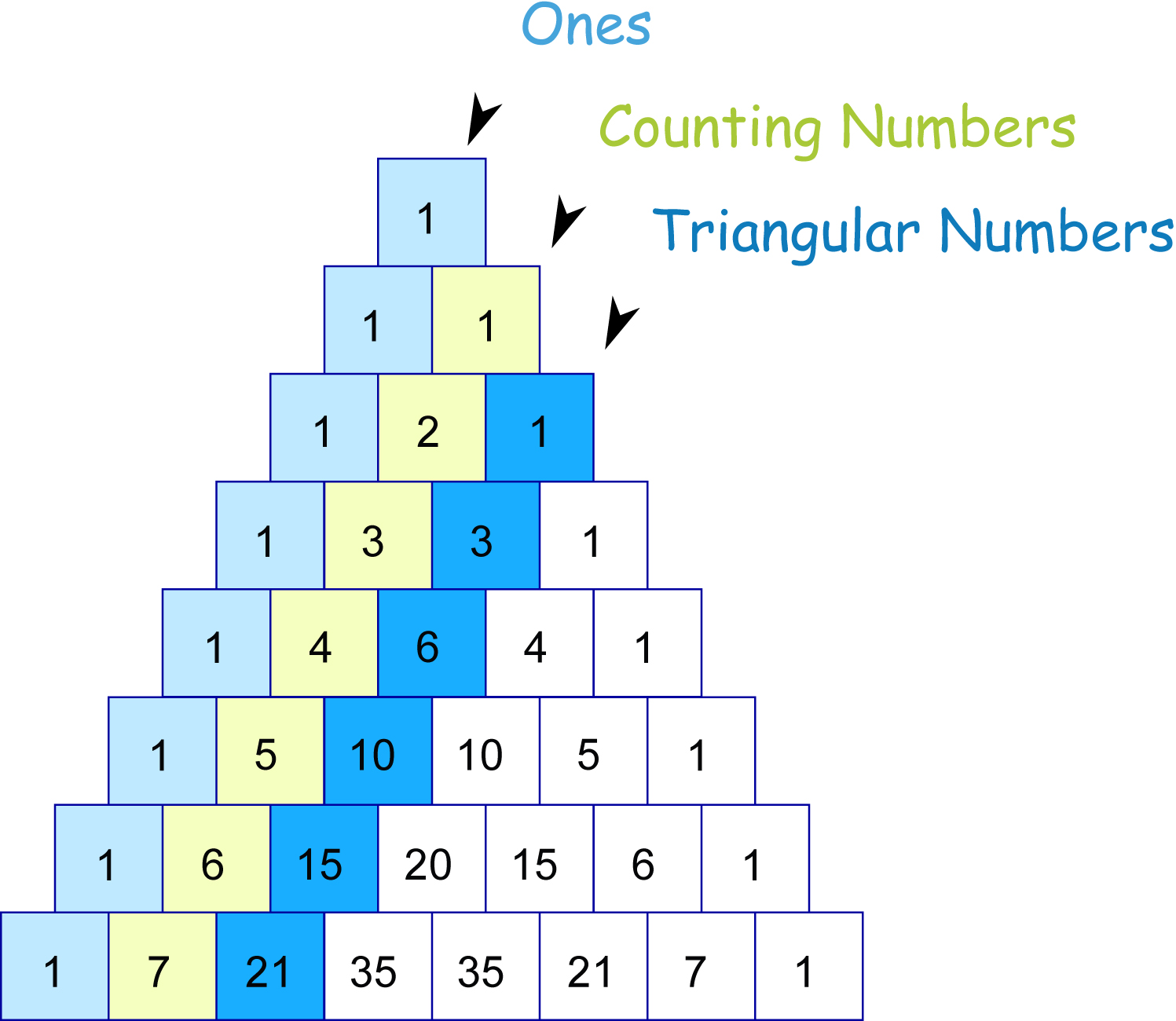
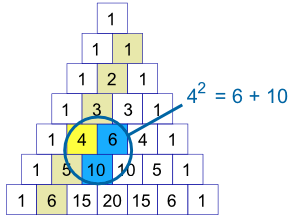
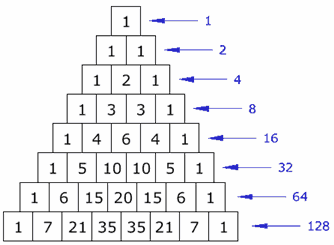
Begin by revisiting with the whole class the patterns that we found in Pascal's Triangle in the Pascal's wager unit in Faith as a Way of Knowing. All images from Math is fun website.

CLASS ACTIVITY II: BUILD A HOUSE OF CARDS
2, 5, 8... The number of cards needed for each of first three levels (rows) of the House of Cards.
Photo WikiHow
Have some packs of playing cards and copious amounts of scratch/rough paper ready in advance.
Students should work in pairs to build a classic House of Cards. A small prize should be awarded to the pair with the most levels that can stand alone for at least 10 seconds!
Next pairs of students should attempt the following tasks:
1. Write, using the fewest possible words, a grammatical prose paragraph that provides definitive instructions to construct a classic house of cards.
2. What is the largest House of Cards that can be made with a single pack of cards?
3. What is the longest single row that can be made with a single pack of cards? (Don't forget the horizontal lids.)
4. Invent or discover a universal formula for total number cards needed to construct a House of Cards with n rows. There are multiple ways to approach this. Be rigorous. Diagram and present your proof succinctly and clearly. Be prepared to present your findings to the entire class.
GOING DEEPER
“When I still ate in a high chair, my father would play a game with me after dinner. He had bought a whole lot of odd rectangular bathroom floor tiles from someplace in Long Island City. We set them up on end one next to the other, and I was allowed to push the end one and watch the whole thing go down...
Next the game improved. The tiles were different colors. I must put one white, two blues, one white, two blues and another white and then two blues… You recognize already the usual insidious cleverness; first delight him in play, and then slowly inject material of educational value! Well, my mother, who is a much more feeling woman, began to realize the insidiousness of his efforts and said, “Mel, please let the poor child put a blue tile if he wants to.” My father said, “No, I want him to pay attention to patterns. It is the only thing I can do that is mathematics at this earliest level.” If I were giving a talk on “what is mathematics?” I would have already answered you. Mathematics is looking for patterns. ”
THE SPECIAL CASE OF MATHEMATICAL INDUCTION
Students already encountered Nobel prize winning physicist, Richard Feynman in Theory of Ignorance and Imagination(with constraints) and living in the subjunctive units, both in Ways of Knowing. A student volunteer should read aloud his wry quote about his own early childhood math training. Ask students whether his definition of mathematics resonated with them as they worked through the House of Cards task.
At least two volunteer groups of students to present their thinking on the House of Cards investigation. It will be interesting to see the various strategies that the collaborative pairs adopted and how they got in the time allocated.
An intriguing clue for finding the general rule for the House of Cards is buried in the diagonals of Pascal's triangle. The triangle numbers are the key to unlocking the puzzle. It is likely that some students will have discovered this and it will have emerged in the presentations and discussion. At first glance nothing could be simpler than the Triangle Numbers. You get them by adding the counting numbers. The general formula is:
You can find expression by a flash of brilliant insight or, more likely, dogged trial and error! When you lay out the number patterns systematically, you should eventually spot that if you take any counting number: add one to it, multiply it by itself, and then divide everything by two, you will obtain the correct cumulative total (of your number and its predecessors) every time.
But trial and error is certainly not proof! It is just ordinary inductive reasoning, where we begin with numerous individual cases and create a general rule. The problem with regular induction is that it works psychologically but lacks the certainty of robust logic. The rule collapses as soon as a single counterexample is found. As trivial as it may sound in the case of adding up the counting numbers, it is just not practical to check every case. The black swan example that we explored in Induction and deduction unit was a vivid illustration of the pitfalls of induction. It was problematic for the tentative real world knowledge of natural science and will hardly serve for the austere perfection abstract mathematics
Fortunately the special case of Mathematical Induction comes to the rescue! This is somewhat confusing because Mathematical Induction is actually a special kind of deductive reasoning with some very specific applications like arithmetic series, and is very handy for investigations like the House of Cards.
Proof by Mathematical Induction has two parts:
1. Show that the expression is valid for the base (smallest) case.
2. Assume that the expression is valid for any case n. Build on that assumption by showing that is valid for the n + 1 case.
This Kahn Academy video contains a thorough and satisfying exposition of the proof.
RESOLUTION OF THE HOUSE OF CARDS
It should be clear by now that each row in the House of Cards requires n pairs for the supports, plus n - 1 horizontal lids. Since we are interested in the total number of cards this boils down to the nth triangle number of pairs, plus the n - 1 triangle number of lids:
A fragment of Euclid's Elements: from the Oxyrhynchus Papyri, excavated from an ancient Egyptian rubbish dump!